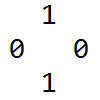上次师院老师给我们上课时出了一道趣题。在一个门上，有一个圆形的转盘，上面有四个开关（上下左右），每次可以抓住两个开关，分别对它进行操作（设置成开或关）。但是圆盘会飞速转动，也就是说，当你的手伸入圆盘时，你可以并且尽可以抓到两个开关；而当你手伸出来后，你无法知道你下一次抓的是什么。当四个开关同为开或同为关，门就会打开。问能否在有限次的操作内打开这扇门？ ↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

答案（最简单的方法貌似不是这样）：

可以的。我可以在7步内解出来。

首先我们规定“抓对角线”表示抓两个不相邻的开关，“抓一条边”表示抓两个相邻的开关。

对于无限的博弈，我们自然希望将无限的状态转为有限的。

那么我们此时就有必胜态：对角线同为0或1，此时抓一次对角线即可通过。

---

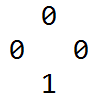再看看一些性质：对于左边这种图形，抓对角线并交换，产生的新状态与旧状态等价（3:1）。

抓一条边并随机将一个置成开，另一个置成关，这样一定可以转换成2:2的状态。

---

对于左边这种图形，抓对角线并交换，产生与旧状态等价的新状态；抓一条边并取反要么可以得到前面的必胜态，要么可以直接打开

---

有了这边这几条规则，就可以通过消去状态来解决问题了。简单的说就是：

1.抓对角线，若两个相同则取反，否则交换。

2.抓一条边，若两个相同则取反，否则交换。

3.抓对角线，若两个相同则取反，否则交换。

4.抓一条边，若两个相同则一开一关，否则交换。

5.抓对角线，若两个相同则取反，否则交换。

6.抓一条边，若两个相同则取反，否则交换。

7.抓对角线，并取反。

每一步都消去一些状态，具体的明天讲讲，今天来不及了。