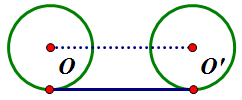
拿两个5毛硬币，一个不动，另一个贴着第一个转，总共转1周，问第二个硬币转了几圈？

这个问题看似很无聊，自己拿硬币试试就知道了（当然我没有一次成功的转满一周，每次都打滑╮(╯▽╰)╭）。实际上，我的第一反应是：肯定不是1圈，2圈差不多，不过也太巧合了吧。然而，生活总是玩弄我们，这种巧合确实存在，事实上答案确实是两圈。然而，生活中的数学问题肯定是有依据的，我们试着从理论层面来分析这个问题。

一个圆绕着另一个圆旋转，这个问题有点复杂，我们不妨将问题化简一下：一个圆在一条线上运动，它运动的距离是多少？

答案很显然，就是圆心所走的距离！由此，我们容易知道，一个圆转动过程中，运动的路程等于圆心运动的路程。有趣的事情发生在一条折线上。

当圆运动到线段的尽头时，它会转向，而此时底部的点是静止不动的。至于怎么转向……我们知道，圆O与第一条线段相切，前进过程中圆始终保持这个状态，相当于以转折点为圆心、圆的半径为半径，做一条弧，运动到圆O’时，圆O’要与第二条线段相切。由此，我们易知：圆O在转折时，运动的距离就是弧O’O的长度（注意，此时圆下面那个点不动，只是“重心转移”）。

说到这里，原来滚硬币的问题应该就很容易解决了。

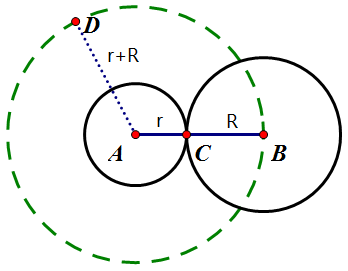
我们推广到一般情况，两个圆，圆A和圆B半径分别是r和R，两圆切与C点，圆B绕着圆A转一周。则圆B运动的路程就是以A为圆心、(r+R)为半径的圆的周长，即2π(r+R)。我们要计算圆B转的圈数，实际上就是除以圆B的周长。所以圆B转的圈数就是：2π(r+R)/2πR即(r+R)/R。对于两个5毛硬币，r=R，所以转的圈数就是(1+1)/1=2圈。

其实我们还可以有更多的玩法，比如说把这个圆放到一个三角形外面。

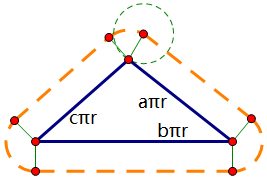
圆的半径为r，三角形三边分别长aπr，bπr，cπr，圆运动的路程就如图中虚线所示。我们可以把它拆成两部分，一部分是(a+b+c)πr，另一部分就是三个弧部分。这三个弧又应该怎么算呢？

生活再次玩弄了我们，这三个弧的角度之和等于360°！原因就是每个条弧所对的角都与三角形的一个角互补，于是乎三条弧度数之和就是(180°-∠A)+(180°-∠B)+(180°-∠C)=180°×3-180°=360°！也就是一个圆，所以三条弧总长2πr。所以圆转动的圈数就=(a+b+c+2)πr/2πr=(a+b+c+2)/2。

当然，你还可以把这个圆扔到抛物线上等等……