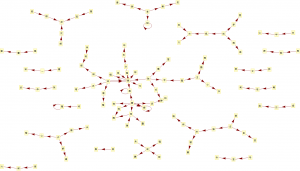
新生报到了,新班级,新名字,新妹子(*^__^*)……我发现我们班“晓某”以及“某萍”很多,似乎能把全班都串起来了。于是我就有种冲动,把名字转成有向图!比方说我叫做甲乙丙,那么就有:甲→乙→丙。当然如此艰巨的任务就得交给Mathematica啦,不过我们需要的首先是一份名表(囧啊,名表是我用手机拍下来,然后自己打的,中间少拍了一段,结果还有10多个人不在名表中- -||)
我把名表保存为.csv文件,简单,易导入。我.csv的格式是:第一行是标题,然后从第二行开始,第一列是号数,第二列是名字。这么说来,在导入Mathematica的时候,就要把第一行和第一列去掉。另外Mathematica导入csv会产生二维List,第一维根据行,第二维根据每行的逗号分隔,比方说:{ {1,甲乙丙},{2,乙丙丁}……}。去掉第一列后变成{ {甲乙丙},{乙丙丁}……},显然我们需要把内括号去掉(也就是把二维降成一维)。导入并处理方法如下:
1
2
3
| A = Flatten[
Drop[Import["C:\Users\Administrator\Desktop\names.csv",
CharacterEncoding -> "UTF-8"], 1, 1]]
|
解释一下,Import用来导入文件,其中CharacterEncoding根据你的文件修改(我乱码了N次)。Import后会产生二维List,用Drop[…,1,1]可以删除第一行和第一列。接着再用Flatten[…]把多维提出来变成一维。现在就把名字存在了A中了。 然后我们要创建一个List B,记录有向图的边,也就是甲→乙→丙。两个For搞定:
1
2
3
4
| B = List[];
For[row = 1, row For[char = 1, char < StringLength[A[[row]]], ++char, B = Append[B, StringTake[A[[row]], {char}] -> StringTake[A[[row]], {char + 1}]]
]
]
|
最后就是画图了,VertexLabeling显示标签,AspectRatio是宽高比,PlotRangePadding是图的内边距,Method是画图算法,DirectedEdges是否显示有向边,MultiedgeStyle是否显示重边,PackingMethod也是画图算法,PlotStyle用来控制点和边的样式:
1
2
3
4
5
| GraphPlot[B, VertexLabeling -> True, AspectRatio -> 0.618,
PlotRangePadding -> 0, Method -> "SpringEmbedding",
DirectedEdges -> True, MultiedgeStyle -> True,
PackingMethod -> "ClosestPackingCenter",
PlotStyle -> {FontFamily -> "Microsoft YaHei", FontSize -> 13}]
|
合起来就是这样:
1
2
3
4
5
6
7
8
9
10
11
12
| A = Flatten[
Drop[Import["C:\Users\Administrator\Desktop\names.csv",
CharacterEncoding -> "UTF-8"], 1, 1]]
B = List[];
For[row = 1, row For[char = 1, char < StringLength[A[[row]]], ++char, B = Append[B, StringTake[A[[row]], {char}] -> StringTake[A[[row]], {char + 1}]]
]
]
GraphPlot[B, VertexLabeling -> True, AspectRatio -> 0.618,
PlotRangePadding -> 0, Method -> "SpringEmbedding",
DirectedEdges -> True, MultiedgeStyle -> True,
PackingMethod -> "ClosestPackingCenter",
PlotStyle -> {FontFamily -> "Microsoft YaHei", FontSize -> 13}]
|
This is it~! 下面偷偷展出我们班的名表有向图(*^__^*) :