[POJ3222]Edge Pairing

这道题觉得十分的厉害，因为看了之后一点想法都没有。不得不Orz Discuss里面的神犇。这题要的是配对，配对这种东西一般是用二分图匹配做的，但是这题完全不懂如何构造出二分图。

Discuss里面的神犇提供了另外一种思路：“图分治”！嗯，这是一个非常神奇的东西，比树分治还神奇。

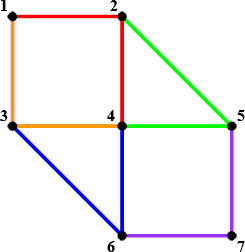
example
example

如果你把一个点u拿出来，然后DFS它所有相邻的点。

对于一个还没有访问过的点v，做完它有2种可能性：

  1. 它剩下一条边(v, w)无法匹配。那我们就构造(u, v, w)这样一对
  2. 它完美的被解决了，那么我们(u, v)这条边就会悬空，不过没关系，我们可以等待下一次发生这样的事情，比方说是(u, s)，那么我们可以配对(v, u, s)

对于一个比u时间戳大的点v，显然我们就不再考虑去做他了，因为他已经做过了。但是(u, v)这条边还是要考虑的，处理方法和上面2一样。

如果一个点结束的时候还有一条边没有配对，那就返回这条边，让调用它的那个点解决，也就是上面的1。

总之是一个非常神的方法。

poj3222Edge Pairing 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

#include <cstdio>

const int MAXN = 20000, MAXM = 100000;
struct Edge
{
  int v;
  Edge *next;
} g[MAXM*2], *header[MAXN];
void AddEdge(const int x, const int y)
{
  static int LinkSize;
  Edge* const node = g+(LinkSize++);
  node->v = y;
  node->next = header[x];
  header[x] = node;
}
int timestamp, n, m, cnt, dfn[MAXN], ans[MAXM/2][3];
int dfs(const int u)
{
  dfn[u] = ++timestamp;
  int v = -1;
  for (Edge *e = header[u]; e; e = e->next)
    if (!dfn[e->v])
    {
      const int w = dfs(e->v);
      if (w != -1)
        ans[cnt][0] = u, ans[cnt][1] = e->v, ans[cnt++][2] = w;
      else if (v != -1)
        ans[cnt][0] = v, ans[cnt][1] = u, ans[cnt++][2] = e->v, v = -1;
      else
        v = e->v;
    }
    else if (dfn[e->v] > dfn[u])
    {
      if (v != -1)
        ans[cnt][0] = v, ans[cnt][1] = u, ans[cnt++][2] = e->v, v = -1;
      else
        v = e->v;
    }
  return v;
}
int main()
{
  scanf("%d%d", &n, &m);
  for (int i = 0, x, y; i < m; ++i)
  {
    scanf("%d%d", &x, &y);
    --x, --y;
    AddEdge(x, y);
    AddEdge(y, x);
  }
  if (dfs(1) == -1)
    for (int i = 0; i < cnt; ++i)
      printf("%d %d %d\n", ans[i][0]+1, ans[i][1]+1, ans[i][2]+1);
  else
    printf("NO");
}

Comments