其实我很早就有自己做一个机器人的想法了，受到两部《Iron Man》的刺激，曾热血沸腾，不过苦于没有经验，不知道从何入手。2010年第1期的《无线电》来了，我欣喜地发现上面有个关于机器人入门的专题。读了这次专题，我才知道，其实机器人也很好做。当然，敢说这句话，只是因为我有单片机基础，至于电子方面的问题，可以和老爸合作。我的想法是做一个最简单的机器人：避撞机器人，说白了就是一只车。

虽说是避撞，但是第一步还是要撞的。我的初步构想是，前面弄一根杆，杆上弄一排微动开关，撞上东西了微动就被触发，电平变化，单片机做出指示：倒退、转弯。等这个作品完成了，再来真正的避撞，大概用红外线来搞吧。

本以为撞只是简单的事情，但看到后面才想起来：电机是模拟的，而单片机输出的信号确是数字的（即要么高电平，要么低电平），无法控制电机的快慢。这才注意到应该用PWM来实现。根据维基百科上面的解释：

脉冲宽度调制（Pulse Width Modulation, 缩写为 PWM），简称脉宽调制，是将模拟信号 转换为脉波的一种技术，一般转换后脉波的周期固定，但脉波的占空比会依模拟信号的大小而改变。

占空比说白了就是在一个周期内，高电位时间占总时间的多少，例如下面，占空比就是T1/T。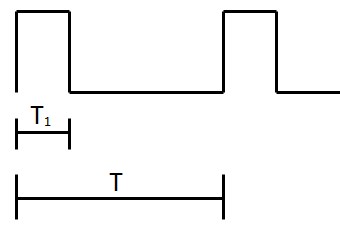

也就是利用占空比，可以调整输出的“电压”，从而来控制模拟器件的运行。要控制直流电机，就要学会PWM！PIC16F877A单片机中带有两路的CCP模块，也就是支持两路PWM。不过这两路共用TMR2计时器，所以它们频率相同，但是可以设置独立的占空比。经过一个早上的奋斗，终于弄懂了基于PIC硬件的PWM。

Read on →

拿两个5毛硬币，一个不动，另一个贴着第一个转，总共转1周，问第二个硬币转了几圈？

这个问题看似很无聊，自己拿硬币试试就知道了（当然我没有一次成功的转满一周，每次都打滑╮(╯▽╰)╭）。实际上，我的第一反应是：肯定不是1圈，2圈差不多，不过也太巧合了吧。然而，生活总是玩弄我们，这种巧合确实存在，事实上答案确实是两圈。然而，生活中的数学问题肯定是有依据的，我们试着从理论层面来分析这个问题。

一个圆绕着另一个圆旋转，这个问题有点复杂，我们不妨将问题化简一下：一个圆在一条线上运动，它运动的距离是多少？

答案很显然，就是圆心所走的距离！由此，我们容易知道，一个圆转动过程中，运动的路程等于圆心运动的路程。有趣的事情发生在一条折线上。

当圆运动到线段的尽头时，它会转向，而此时底部的点是静止不动的。至于怎么转向……我们知道，圆O与第一条线段相切，前进过程中圆始终保持这个状态，相当于以转折点为圆心、圆的半径为半径，做一条弧，运动到圆O’时，圆O’要与第二条线段相切。由此，我们易知：圆O在转折时，运动的距离就是弧O’O的长度（注意，此时圆下面那个点不动，只是“重心转移”）。

说到这里，原来滚硬币的问题应该就很容易解决了。 Read on →

其实就是上一篇的四开关问题。昨天师院老师来讲课时又提了一下，只要5步就可以解出来了。

题目：在一个门上，有一个圆形的转盘，上面有四个开关（上下左右），每次可以抓住两个开关，分别对它进行操作（设置成开或关）。但是圆盘会飞速转动，也就是说，当你的手伸入圆盘时，你可以并且尽可以抓到两个开关；而当你手伸出来后，你无法知道你下一次抓的是什么。当四个开关同为开或同为关，门就会打开。问能否在有限次的操作内打开这扇门？

解法：

Read on →

上次师院老师给我们上课时出了一道趣题。在一个门上，有一个圆形的转盘，上面有四个开关（上下左右），每次可以抓住两个开关，分别对它进行操作（设置成开或关）。但是圆盘会飞速转动，也就是说，当你的手伸入圆盘时，你可以并且尽可以抓到两个开关；而当你手伸出来后，你无法知道你下一次抓的是什么。当四个开关同为开或同为关，门就会打开。问能否在有限次的操作内打开这扇门？ Read on →

如题，证明任意个正方形可以通过适当的裁剪，拼成一个大正方形。

出自我们的一张竞赛卷，据说是外国的一道竞赛题，题目很巧妙。开始时百思不得其解，结果讲评用30秒就解决了。 Read on →